Fitbitデータでスパース推定に入門してみる④　〜Graphical lassoで変数間の関係性について調べる〜

はじめに

これまで述べてきたのは、主にモデルの回帰係数の推定に基づく話でした。

mikutaifuku.hatenablog.com

今回のエントリでは、これまでの回帰係数の推定ではなく、共分散構造に注目した手法を取り上げます。多数の変数間の依存関係を推定するために、ガウシアングラフィカルモデルにL1正則化の考え方を応用する、Graphical lassoとよばれる手法を使います。なお、今回の記事も今までと同様に以下の書籍（5.1 グラフィカルモデルにおけるスパース推定）を参考に書いたものですので、詳細は書籍を参考にしていただければと思います。

スパース推定法による統計モデリング (統計学One Point)

作者: 川野秀一,松井秀俊,廣瀬慧
出版社/メーカー: 共立出版
発売日: 2018/03/08
メディア: 単行本
この商品を含むブログを見る

ガウシアングラフィカルモデル

$X = (X_1, ..., X_p)^{T}$ が多変量正規分布 $N( \boldsymbol{\mu} ,\Sigma)$ に従うとき、変数 $X_j$ と $X_k$ の関係性を推定し、それをグラフ化する手法です。分散共分散行列の逆行列 $\Omega = \Sigma^{-1}$ とし、 $\Omega$ の $(j, k)$ 成分を $w_{jk}$ とします。詳細は書籍に譲りますが、 $w_{jk} = w_{kj} = 0$ の時に、 $X_j$ と $X_k$ は他の変数を与えた元で条件付き独立と言います。

データ分析でよくみられる相関係数は、他の変数からの影響も含めて測っているのに対して、行列 $\Omega$ は他の変数からの影響を除いて、（すなわち $X_j$ と $X_k$ 以外の変数の条件のもとで）関連の強さを測るものになります。

例えば、以下のような行列 $\Omega$ （左図）が得られている場合は、右のようなグラフで条件付き独立性の有無を表現することができます*1。

f:id:mikutaifuku:20180323152702p:plain

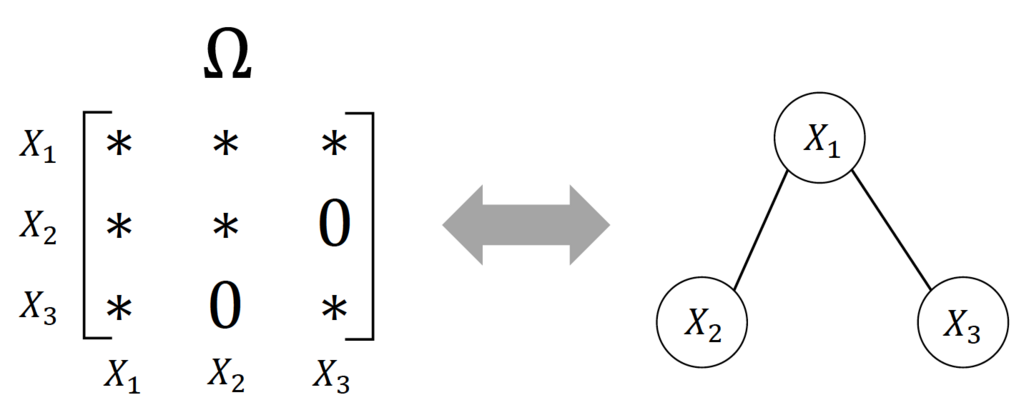
このグラフが表現するのは「条件付き独立性」があるか否かということだけであって、「変数間の関係の向き」を推定することができません。もし、グラフの辺の向きを推定したい場合は、以前紹介したようにLingamモデルを仮定することで推定することができます。

mikutaifuku.hatenablog.com

パラメータ推定

グラフの辺の数は最大で頂点の２乗のオーダー程度になりますが、実際に辺が存在する数は少ないという意味ではスパースと言えます。データからスパースな分散共分散行列の逆行列（精度行列） $\Omega$ を推定する手法をgraphical lassoと言います。データ $\boldsymbol{x_1} , … ,\boldsymbol{x_n}$ が観測され、これらが正規分布に従っていると仮定します。この時、標本から計算される分散共分散行列をSとすると、対数尤度関数に基づく損失関数は、

f:id:mikutaifuku:20180323172632p:plain:w220

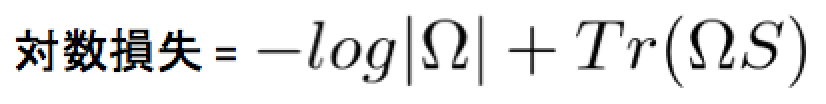
となります（定数省略）*2。これに $L_1$ 正則化項 $\Sigma_{j,k} |w_{jk}|$ を加えた式を最小化にすることで、精度行列 $\Omega$ を推定します。

f:id:mikutaifuku:20180323173357p:plain:w250

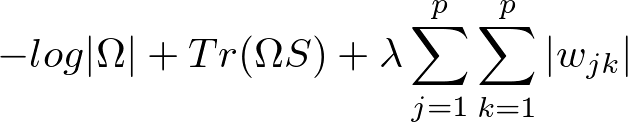
Rでやってみた

データ

Fitbitデータから得られる

efficiency：睡眠効率
timeInBed：ベッドにいた時間
sedentaryMinutes：座っている時間
restingHeartRate：安静時心拍数
steps：歩数
caloriesOut：消費カロリー

の項目を使用しました。

> glimpse(d)
Observations: 210
Variables: 6
$ efficiency       <int> 94, 95, 96, 97, 98, 94, 96, 98, 97, 99, 99, 95, 98, 97, 97, 97, 97, ...
$ timeInBed        <int> 413, 444, 568, 531, 308, 718, 332, 329, 303, 309, 309, 283, 295, 359...
$ sedentaryMinutes <int> 884, 660, 669, 717, 658, 797, 653, 905, 941, 925, 943, 530, 1033, 94...
$ restingHeartRate <int> 67, 64, 64, 65, 65, 65, 66, 67, 68, 67, 68, 67, 67, 66, 67, 68, 69, ...
$ steps            <int> 6488, 17042, 18910, 7970, 9075, 9175, 2161, 10136, 8588, 10373, 8997...
$ caloriesOut      <int> 2585, 3583, 3573, 2737, 3060, 3409, 2188, 2986, 2790, 2950, 2842, 25...

散布図行列を作成し、データの傾向をみてみます*3。コードはこのブログの最後に載せています。

f:id:mikutaifuku:20180323212010p:plain

歩数と消費カロリー（５行６列）は相関係数が0.92と強い正の相関があります。
睡眠効率とベッドにいた時間（１行２列）は相関係数が-0.16とやや負の相関があります。ベッドにだらだらと長い間居ると、睡眠効率が悪くなりそうなことから容易に想像がつきます。
ベッドにいた時間と座って居る時間が（２行３列）は相関係数が-0.11とやや負の相関があります。普通に考えてベッドに長くいれば（≠座っている状態）、座る時間も短くなりそうです。
睡眠効率と消費カロリー（１行６列）は相関係数が0.18とやや正の相関があります。消費カロリーが大きい日（よく歩いたり、運動したりした日）は、効率の良い睡眠が取れてそうです。

というように、この結果からも色々なことが考えられます。（もっと色々相関があってほしかった…）

graphical lasso

glassoパッケージを使用します。プログラムはものすごく単純です*4。

library(glasso) 
library(igraph)  # グラフを描くのに必要

cordat <- cor(d)
fit.glasso <- glasso(cordat, rho = 0.4)
fit.glasso$wi  # 共分散逆行列

makeadjmat <- function(mat, cordat) {
  ans <- mat
  diag(ans) <- 0
  ans <- ans != 0
  ans <- matrix(as.numeric(ans), nrow(ans), nrow(ans))
  colnames(ans) <- rownames(ans) <- colnames(cordat)
  ans
}
adjmat <- makeadjmat(fit.glasso$wi, cordat)  # 隣接行列
g <- graph.adjacency(adjmat, mode = "undirected") 
plot(g,vertex.size = 70, vertex.shape = "rectangle", vertex.color = "white")

λ=0.1の時のグラフィカルモデルです

f:id:mikutaifuku:20180323222606p:plain

λ=0.4の時のグラフィカルモデルです。 f:id:mikutaifuku:20180323222627p:plain

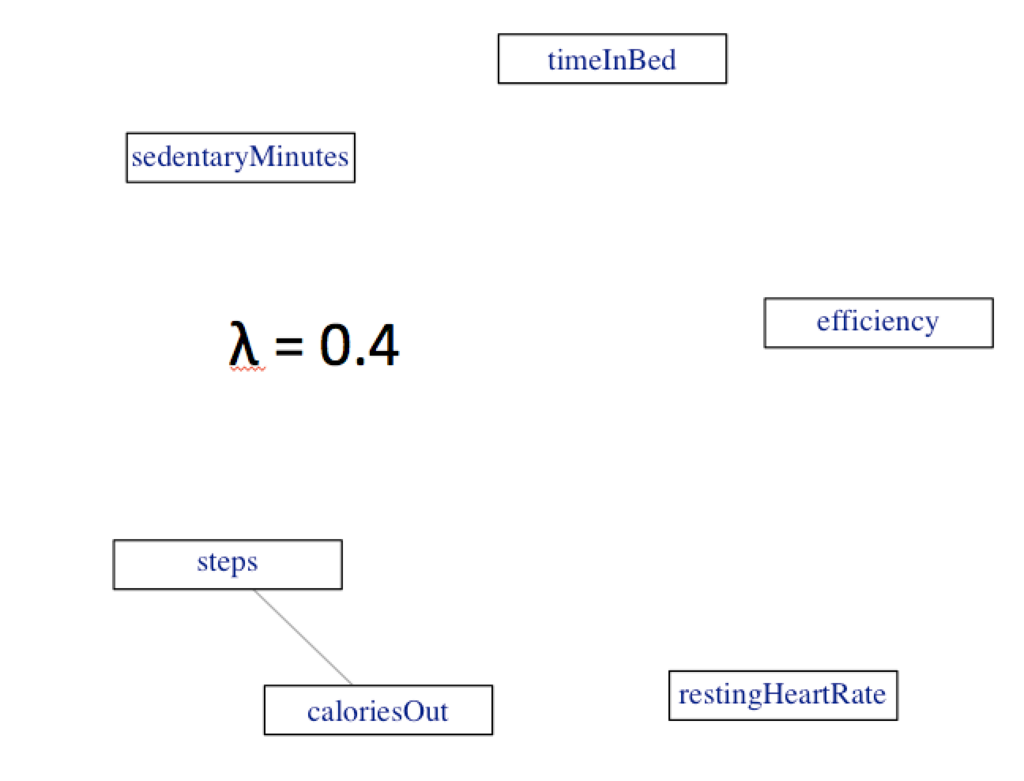
安静時心拍数（RestingHeartRate）はどの変数とも関係がなさそうです。
歩数（steps）と消費カロリー（caloriesOut）は関係がありそうです。

推定された $\Omega$ から、偏相関係数という量を算出して、可視化することもできますが、次回の機会にとっておきます。

相関行列の可視化Rコード

library("ggplot2")
library("ggthemes")
library("scales")
library("GGally")

N_col <- ncol(d)
ggp <- ggpairs(d, upper='blank', diag='blank', lower='blank')

for(i in 1:N_col) {
  x <- d[,i]
  colnames(x) <- "tmp_name"
  p <- ggplot(x, aes(tmp_name))
  p <- p + theme(text=element_text(size=14), axis.text.x=element_text(angle=40, vjust=1, hjust=1))
  bw <- (max(x)-min(x))/10
  p <- p + geom_histogram(binwidth=bw, color='darkgrey', fill='darkgrey', alpha=0.5)
  p <- p + geom_line(eval(bquote(aes(y=..count..*.(bw)))), stat='density', alpha=0.5)
  p <- p + geom_label(data=data.frame(x=-Inf, y=Inf, label=colnames(d)[i]), aes(x=x, y=y, label=label), hjust=0, vjust=1) 
  p <- p + theme_bw() + scale_color_pander()
  ggp <- putPlot(ggp, p, i, i)
}

zcolat <- seq(-1, 1, length=81)
zcolre <- c(zcolat[1:40]+1, rev(zcolat[41:81]))

for(i in 1:(N_col-1)) {
  for(j in (i+1):N_col) {
    x <- as.numeric(unlist(d[,i]))
    y <- as.numeric(unlist(d[,j]))
    r <- cor(x, y, method='spearman', use='pairwise.complete.obs')
    zcol <- lattice::level.colors(r, at=zcolat,
                                  col.regions=colorRampPalette(c(scales::muted('red'), 'white', scales::muted('blue')), space='rgb')(81))
    textcol <- ifelse(abs(r) < 0.4, 'grey20', 'white')
    ell <- ellipse::ellipse(r, level=0.95, type='l', npoints=50, scale=c(.2, .2), centre=c(.5, .5))
    p <- ggplot(data.frame(ell), aes(x=x, y=y))
    p <- p + theme_bw() + theme(
      plot.background=element_blank(),
      panel.grid.major=element_blank(), panel.grid.minor=element_blank(),
      panel.border=element_blank(), axis.ticks=element_blank()
    )
    p <- p + geom_polygon(fill=zcol, color=zcol)
    p <- p + geom_text(data=NULL, x=.5, y=.5, label=100*round(r, 2), size=6, col=textcol)
    ggp <- putPlot(ggp, p, i, j)
  }
}

for(j in 1:(N_col-1)) {
  for(i in (j+1):N_col) {
    x <- d[,j]
    y <- d[,i]
    colnames(x) <- "tmp_x_name"
    colnames(y) <- "tmp_y_name"
    p <- ggplot(data.frame(x, y), aes(x=tmp_x_name, y=tmp_y_name))
    p <- p + theme(text=element_text(size=14), axis.text.x=element_text(angle=40, vjust=1, hjust=1))
    p <- p + geom_point(size=1, color='darkgrey', fill='darkgrey', alpha=0.5)
    p <- p + theme_bw() + scale_color_pander()
    p <- p + theme(text=element_text(size=14), axis.text.x=element_text(angle=40, vjust=1, hjust=1))
    ggp <- putPlot(ggp, p, i, j)
  }
}

print(ggp)

さいごに

今回のエントリでは、graphical lassoという手法を用いてFitbitデータの変数間の関係性をみました。またgraphical lassoによる異常検知の手法というのも存在しているらしく、相当変なデータを使用してもおかしな結果を出しにくいという意味で実用性が高いらしいので*5、機会があればチャレンジしてみようかと思います。

ということで、４回に渡ってスパース推定入門エントリを書いてきましたが、このシリーズは一旦これにて終わりにしようと思います。今回はスパース推定法による統計モデリング (統計学One Point)の本を読んで自分なりに整理したわけですが、計算アルゴリズムを飛ばしたり、式を手計算できっちりと追いかけた訳ではないので、時間を見つけて再勉強しようと思います。

短時間で書いたので間違いがあるかもしれません。その際は優しくご指摘いただきますと幸いです。

mikutaifuku

*1:書籍p.107を参考に書きました

*2:詳細な計算手順等は書籍を参考してください

*3:散布図行列を描くには（corrplot, pairs, GGally） - StatModeling Memorandumの記事を参考にさせて頂きました。本当にすごいですね。

*4:書籍に書かれていたものを写しました

*5:岩波データサイエンス Vol.5に書いていました

mikutaifukuの雑記帳

個人的な雑記帳。データ分析とか読んだ本の感想とか。